\(\newcommand{\g}{\boldsymbol{\gamma}} \newcommand{\R}{\mathbb{R}}\) I was revising some calculus/mechanics from undergrad the other day and came across the arc length formula: given a differentiable curve \(\g: [a,b] \to \R^n\), the length of the curve is \[ L(\g) = \int_a^b ||\g’(t)|| \, dt \text{.} \] That is to say if I straightened out \(\g\), I would have a line of length \(L(\g)\). I had used this formula plenty of times, but I realised that I had no intuition for why it was true, so I had a Think.

Our lovely curve

I figured that if I was wanted to estimate the length of the curve by hand, I could split it up into smaller sections and approximate the length of each by the length of the line joining the two endpoints. So I partitioned my interval \([a,b]\) into \(N-1\) chunks of size \(\Delta t = (b-a)/N\), so the endpoints are \(\{t_i: \, i = 0,\dots, N\}\), where \(t_i = a + i\Delta t\), and used that to split up the curve.

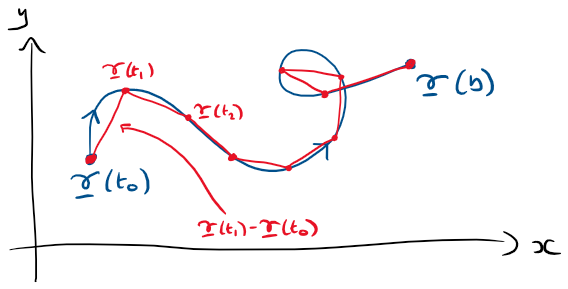
Lovely curve chopped up

So now our approximate length is \(L(\g) \approx \sum_{i=0}^{N-1} ||\g(t_{i+1}) - \g(t_i)||\). This is starting to look like what we want - remember that an integral is approximately \(\int_a^b f(t) dt \approx \sum_i f(t_i) \Delta t\). Since we need some \(\Delta t\) term in our sum we can just multiply by 1 to get \(L(\g) \approx \sum_{i=0}^{N-1} \frac{||\g(t_i + \Delta t) - \g(t_i)||}{\Delta t}\Delta t\). We see from our previous figure that as \(\Delta t \to 0\), we will get closer to the true arc length, so we get that \[\begin{align} L(\g) &= \lim_{\Delta t \to 0} \sum_{i=0}^{N_{\Delta t}-1} \left\lVert\frac{\g(t_i + \Delta t) - \g(t_i)}{\Delta t}\right\rVert \Delta t \\ &= \int_a^b ||\g’(t)|| \, dt \text{,} \end{align} \] by the definition of the derivative and the integral. Pretty neat!

p.s. Happy \(\pi\) day!